SDPAとその派生版
| 名前 |
説明 |
| SDPA |
基本バージョン |
| SDPA-M |
SDPA を Matlab 上から動かす |
| SDRARA |
SDPA の並列計算 (MPIを使用) |
| SDPA-C |
SDPA に行列補完理論を導入 |
| SDPARA-C |
SDPA-C の並列計算 |
| SDPA-CG |
SDPA の線形方程式系に共役勾配法を適用 (非公開) |
| SDPA-R |
SDPA の安定性を高める (非公開) |
| SDPA-S |
多くのブロック対角を持つ SDP を効率良く解く (非公開) |
とりあえず解いてみる
NEOS server 上の SDPA を使って半正定値計画問題を解く手順について説明します。 例として、以下のSDP問題を解いてみましょう。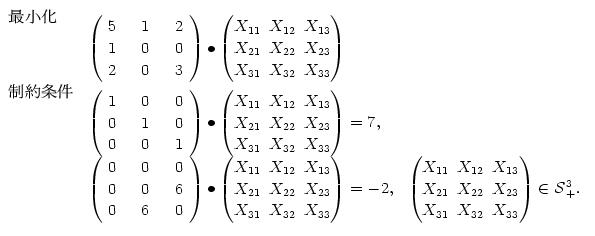
- 問題を SDPA sparse format で記述します。
- 以下のような感じになります。実際の入力データファイルはこちら
- 詳しい説明はSDPAのマニュアルを参照して下さい
2 ← 線形制約の数
1 ← とりあえず1にする
3 ← 行列の次元
7 -2 ← 線形制約の右辺の値を順番に並べる
0 1 1 1 5 ↓ 以下では行列に関して記述する
0 1 1 2 1 一行が行列の非ゼロ要素一つに対応し、k番目の行列の
0 1 1 3 2 (i,j)要素の値が v のとき、k 1 i j v と並べる。
0 1 3 3 3 ただし、
1 1 1 1 1 ・目的関数に現れる行列は、0番目と考える
1 1 2 2 1 ・対称行列なので、上半分(対角を含む)のみ記述する
1 1 3 3 1
2 1 2 3 6
- NEOS server に問題を送る
- http://neos.mcs.anl.gov/neos/solvers/sdp:SDPA/SPARSE_SDPA.html に飛ぶ
- SDPA data(local file): の欄に入力データファイル名を入れる
- Submit to NEOS をクリック
- しばらく待つと結果が表示される(上の問題ならば数秒で解けます)
もし 2.で e-mail address: の欄に自分のメールアドレスを入力しておけば、結果がメールでも送られてきます
- 出力結果を調べる
このような画面が現れますが、大事な部分は以下の項目です。 (詳細はSDPAのマニュアルを参照して下さい)
- phase.value = pdOPT ならば解けています
- gap
=
誤差の上界です
- objValDual = 最適値です
-
yMat = 最適解です
つまり、この問題の最適値は 4.3039951985e+01 で、最適解は{ {+4.916e+00, -2.568e-01, +3.191e+00 },という行列になります。
{-2.568e-01, +1.341e-02, -1.667e-01 },
{+3.191e+00, -1.667e-01, +2.071e+00 } }
- phase.value = pdOPT ならば解けています